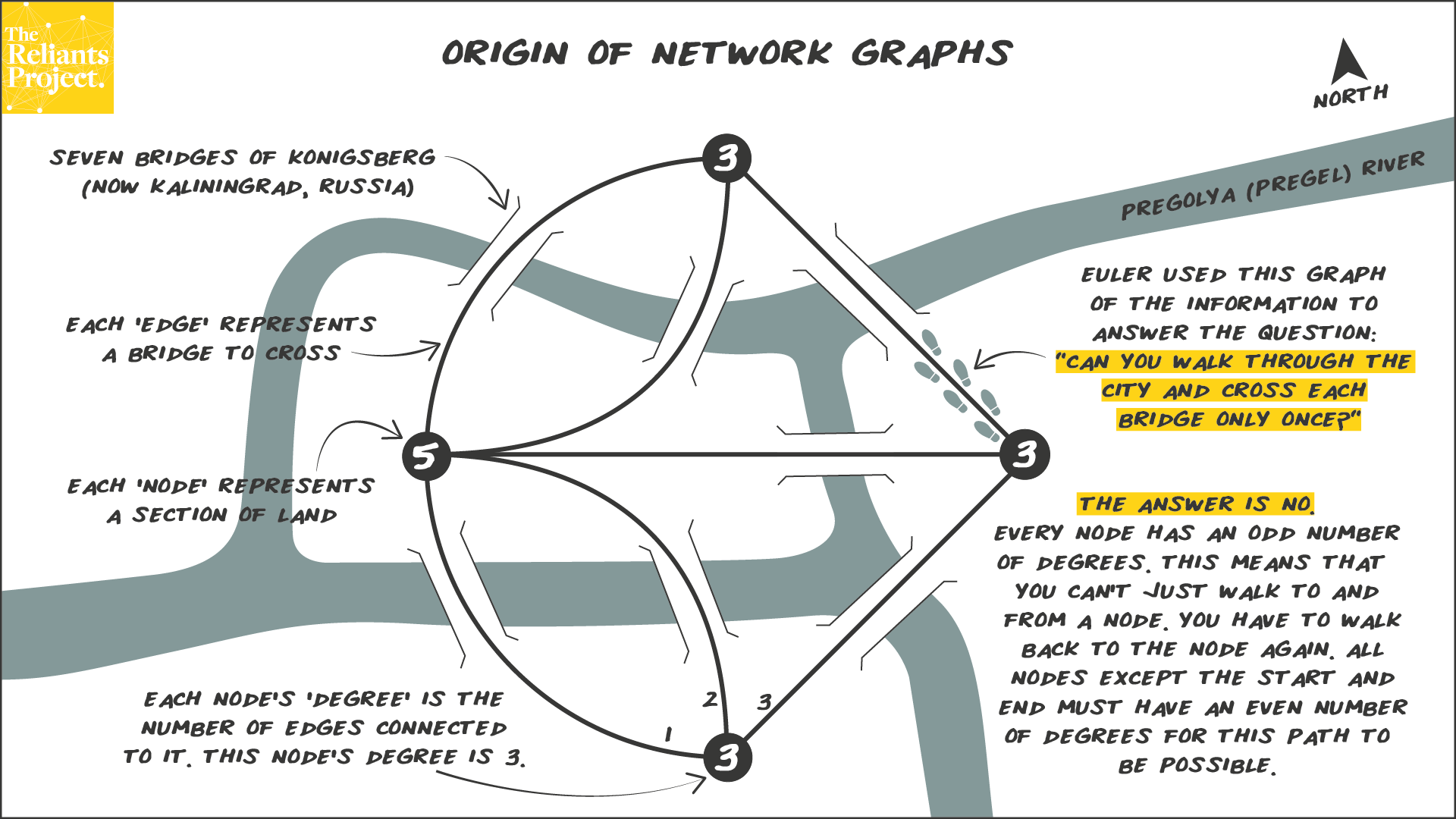
The idea of showing information as a network graph had to come from somewhere. Turns out it began as a very relatable problem. No one likes to retrace their steps when taking a walk. Whether you’re in your own neighbourhood, visiting a new city or a trail in the mountains, we usually prefer to take a unique path that allows us to visit all the points of interest without walking on the same stretch twice.

The residents of Königsberg (now Kaliningrad, Russia) wanted to do the same. In 1736, they had 7 beautiful bridges that crossed the Pregel (now Pregolya) river between 4 different parts of the city. There were parts of the city north of the river, south of the river, east of the river and an island in the centre. They wondered if they could walk through the 4 parts of the city and cross each of the 7 bridges only once.

In order to solve the problem, mathematician Leonhard Euler decided to visualise the information as a network graph. Each edge represented one bridge and each node represented one part of the city. That’s how he came up with this graph of 7 edges connecting 4 nodes. The number of edges connected to each node is called the degree. In this graph, there are 3 nodes with a degree of 3, meaning 3 edges connected to each of them. There is one node with a degree of 5.

He then realised an important thing about the degree of each node:

1. If you walk over one bridge to the north of the river, that counts as 1 degree, an odd number.
2. If you then walk south over a second bridge, that counts as 2 degrees, an even number.
3. If you then walk north again over a third bridge, that counts as 3 degrees, an odd number again.
4. At this point, it is impossible to walk south without retracing your steps because there is no new bridge to cross.
5. If this is the case, a part of land (node) with an odd number of bridges connected to it (degrees) can only serve as the start or end of a walk.
6. All the other stops (nodes) along the way need to have an even number of bridges connected to it (degrees) so that you can arrive and leave without retracing your steps.

Since this graph only has land (nodes) with an odd number of bridges connected to it (degrees), he correctly concluded that it would be impossible to find a path where you didn’t have to retrace your steps.

Ready for the next concept? The next one in the series is Concept 2: How to Read Graphs Using The Empire Strikes Back.